
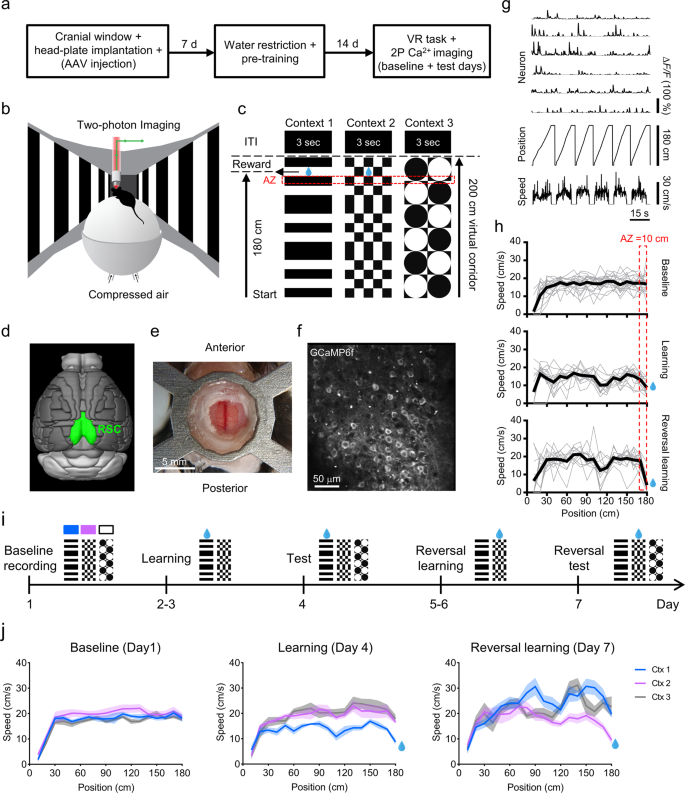
At this point, the total variance on all of the principal components will equal the total variance among all of the variables. This continues until a total of p principal components have been calculated, that is, the number of principal components is the same as the original number of variables. The second principal component is calculated in the same way, with the conditions that it is uncorrelated with (i.e., perpendicular to) the first principal component and that it accounts for the next highest variance.

To prevent this, the sum of squares of the weights is constrained to be 1. Of course, one could make the variance of Y 1 as large as possible by choosing large values for the weights a 11, a 12.

The first principal component is calculated such that it accounts for the greatest possible variance in the data. The first principal component (Y 1) is given by a linear combination of the variables X 1, X 2. Doing this insures that the cloud of data is centered on the origin of our principal components, but it does not affect the spatial relationships of the data nor the variances along our variables. Typically, the first step is to center the data on the means of each variable, accomplished by subtracting the mean of a variable from all values of that variable. There should be no missing values: every variable should have a value for every sample, and this value may be zero. The data set should be in standard matrix form, with n rows of samples and p columns of variables. PCA produces linear combinations of the original variables to generate the axes, also known as principal components, or PCs. The formal name for this approach of rotating data such that each successive axis displays a decreasing amount of variance is known as Principal Components Analysis, or PCA. For example, you might start with thirty original variables, but might end with only two or three meaningful axes. This is known as reducing the dimensionality of a data set. For data sets with many variables, the variance of some axes may be great, whereas the variance on others may be so small that they can be ignored. When dealing with many variables, this process allows you to assess any relationships among variables very quickly. In this simple example, these relationships may seem obvious. These axes contain information from our original variables, but they do not coincide exactly with any of the original variables. Axis 2 could be regarded as a measure of shape, with samples at any axis 1 position (that is, of a given size) having different length to width ratios. In this example, axis 1 could be interpreted as a size measure, likely reflecting age, with samples on the left having both small length and width and samples on the right having large length and width. Mathematically, the orientations of these axes relative to the original variables are called the eigenvectors, and the the variances along these axes are called the eigenvalues.īy performing such a rotation, the new axes might have particular explanations. Finally, note that our new vectors, or axes, are uncorrelated. Also note that the spatial relationships of the points are unchanged this process has merely rotated the data. In this new reference frame, note that variance is greater along axis 1 than it is on axis 2. Once we have made these vectors, we could find the coordinates of every data point relative to these two perpendicular vectors and re-plot the data, as shown here (both of these figures are from Swan and Sandilands, 1995). Both vectors are constrained to pass through the centroid of the data.
We could pass one vector through the long axis of the cloud of points, with a second vector at right angles to the first. The two are highly correlated with one another. Suppose we had measured two variables, length and width, and plotted them as shown below. Principal Components Analysis Introduction


 0 kommentar(er)
0 kommentar(er)
